Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2 174454

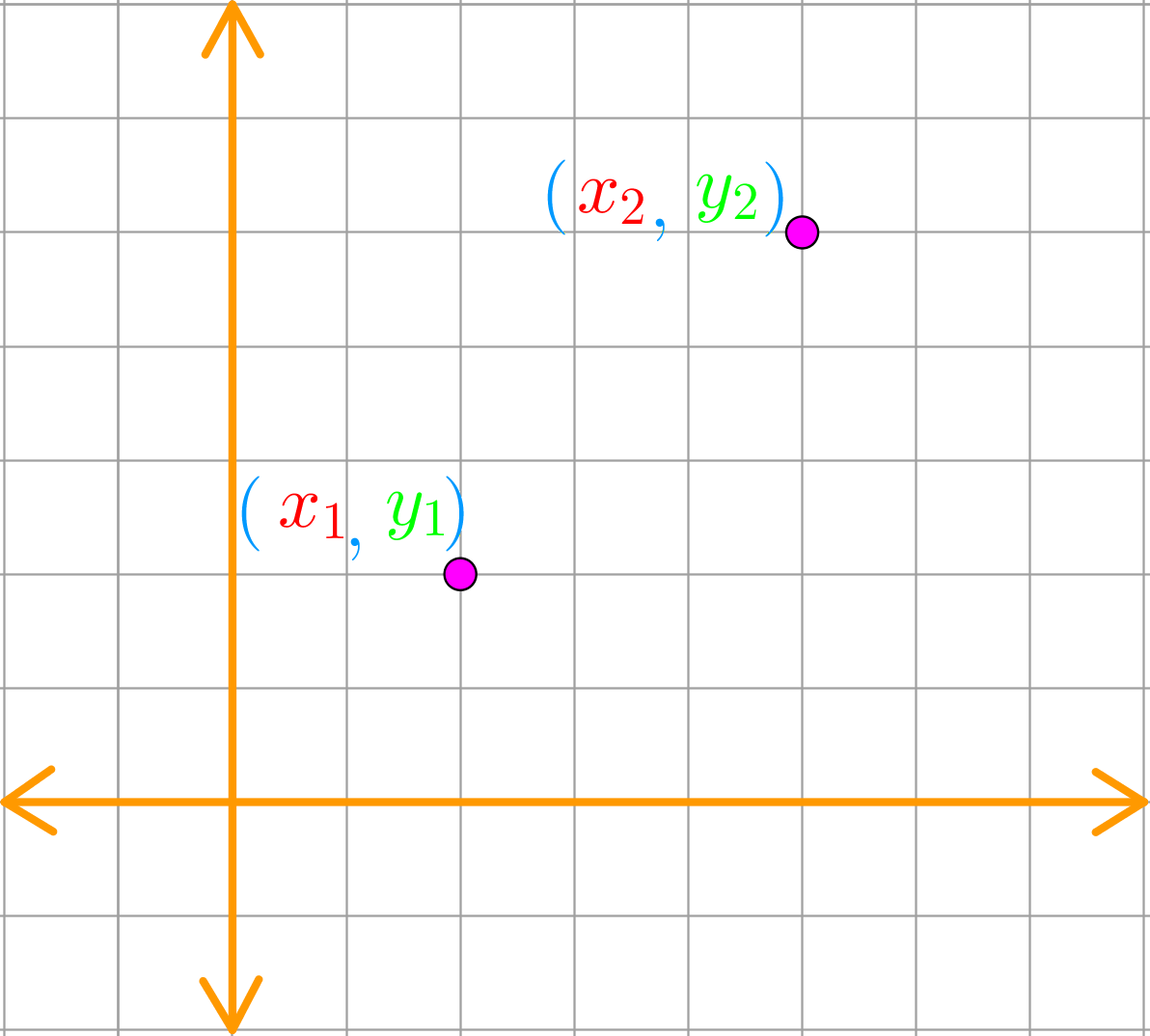
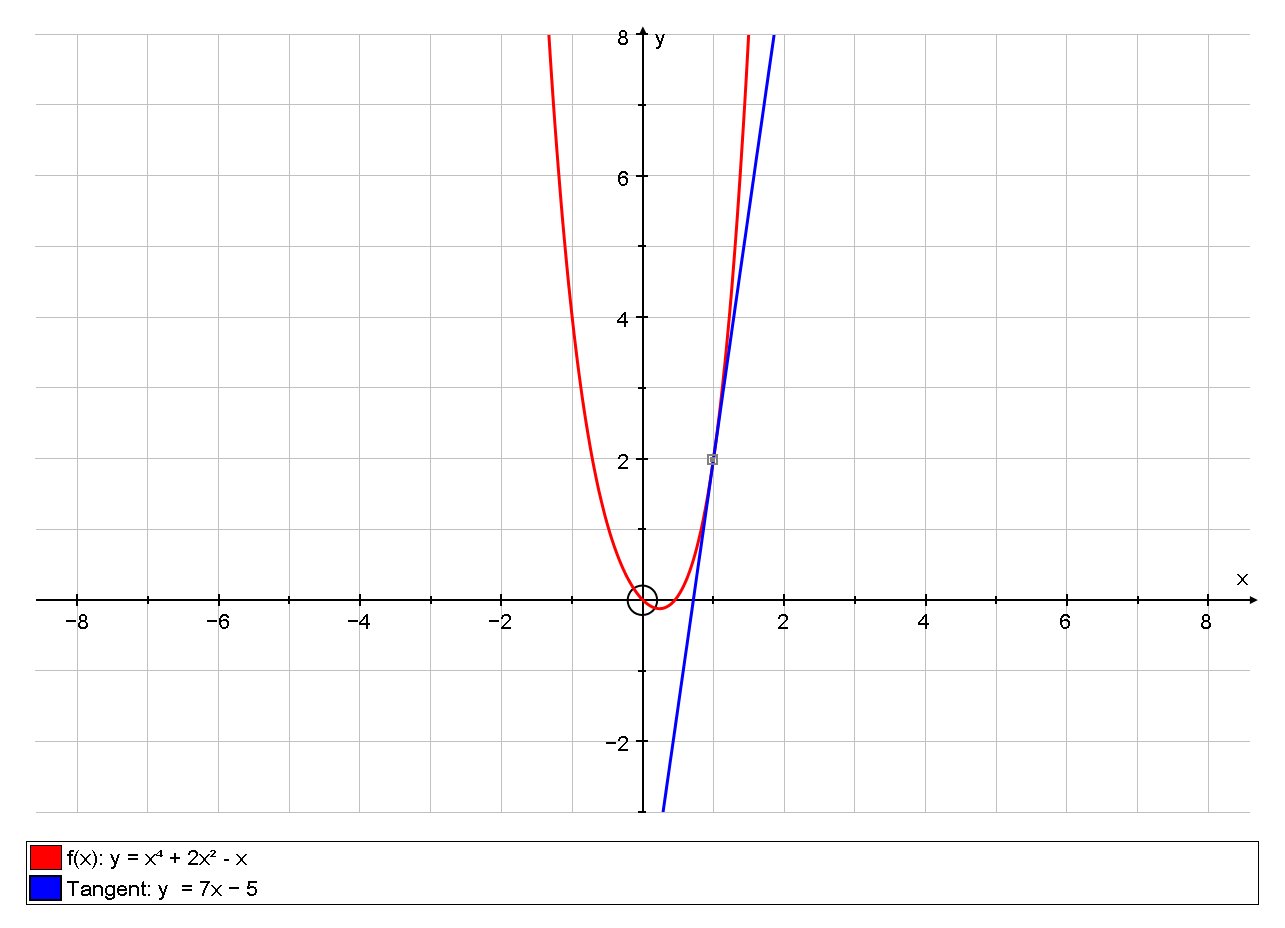
 Question 28 (OR 1st Question) If √(1−𝑥^2 ) √(1−𝑦^2 ) = a (x − y), then prove that 𝑑𝑦/(𝑑𝑥 ) = √(1 − 𝑦^2 )/√(1 − 𝑥^2 ) Finding 𝒅𝒚/𝒅𝒙 would be complicated here To make life easy, we substitute x = sin A y = sin B (As √(1−𝑥^2 )= √(1−sin^2⁡𝐴 )=√(cos^2⁡𝐴 )) And then solve Let's substitute x

Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2- 1 First make the equation into x^22x1 >= 0 by rearranging and multiplying by x You should find it is (x1)^2 so for any x (not just x>0) this function is greater than or equal to 0 because of ^2 For your situation it is obvious that x>0 which is certainly true for the factorised function Therefore you have proved that x1/x is greaterExample 1 X and Y are jointly continuous with joint pdf f(x,y) = ˆ cx2 xy 3 if 0 ≤ x ≤ 1, 0 ≤ y ≤ 2 0, otherwise (a) Find c (b) Find P(X Y ≥ 1) (c) Find marginal pdf's of X and of Y (d) Are X and Y independent (justify!) (e) Find E(eX cosY) (f) Find cov(X,Y) We start (as always!) by drawing the support set (See below, left) 2 1 2 1 1 x y=1−x y x y support set

Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Show That X 1 Y 1 X 1 X 1 Y 1 Y 1 X2 Y2 Xy Maths Number Systems Meritnation Com
If 1 X 2 1 Y 2 A X Y Then Prove That Dy Dx
If 𝟐 𝒙 𝟑 𝒚 𝟏𝟐 𝒛 Show That 𝟏 𝒛 𝟏 𝒚 𝟐 𝒙 Youtube
If Y Xx Prove That D2y Dx2 1 Y Dy Dx 2 Y X 0 Explain In Great Detail Cbse Class 12 Learn Cbse Forum
Free Math Answers Answers Within 24 Hours Step By Step Explanations
If Y X X2 1 1 2 M Then Show That X2 1 D2y Dx2 X Dy Dx M2y 0 Mathematics Topperlearning Com 6jd9kell
Solved 40 Lim Xy 2 E 1 X2 Y2 X Y 0 0 X2y2 141 Lim Chegg Com
If X 1 Y 2 Y 1 X 2 1 Prove That Dydx 1 Y 2 1 X 2
Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
1 2 4 8 Wikipedia
Answered Q1 Solve 1 Lim X 2n 2x 4n 2 Lim Bartleby
7 If Dfrac511abarb 1 Pro Ea See How To Solve It At Qanda
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube
Math 12 Solution Book Ptb V 1 For Android Apk Download
7 7 The Inverse Hyperbolic Functions
Continuity And Differentiability Class 12 Ncert Solutions
Which Expression Is Equivalent To X 1 2y 1 4z 2 A X 1 2 Yz 2
If 2 X 3 Y 12 Z Then Prove That Xy Z X 2y Mathematics Topperlearning Com 8v1liiww
Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples
If Y X 1 X Show That X 2dy Dx Xy 2 0 Brainly In
Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com
If Sin 1x Sin 1 Y Sin 1 Z Pie Prove Thata X Root 1 X2 Y Root 1 Y2 Z Root 1 Z2 2xyz Edurev Class 12 Question
Univasf Edu Br
Division By Zero Wikipedia
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Cos Inverse 1 X 2 1 X 2 Formula Resepahmantab
Distance Formula Expii
If Y X Sin 1 X 1 X 2 Prove That 1 X 2 Dy Dx X Y X Edurev Class 12 Question
If X 1 Y Y 1 X 0 1 X 1 Prove That Dy Dx 1 1 X 2 Sarthaks Econnect Largest Online Education Community
最も好ましい V Yzy 7112 V 3x 2 Y 5 X 4 Y 4 Irasutoaokkc
Step By Step Solutions
Covering Non Uniform Hypergraphs Endre Boros Yair Caro Zoltan
If Xy Ex Y Prove That From Continuity And Differentiability Class 12 Cbse
What Is The Formula For Finding Distance Studypug
Graph Graph Inequalities With Step By Step Math Problem Solver
If 1 X 2 1 Y 2 A X Y Then Prove That Dy Dx
If X 2 X 1 Y 2 Y 1 X 2 X 1 Y 2 Y 1 Show That Xy 1 Mathematics Topperlearning Com Mbpqbwdd
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

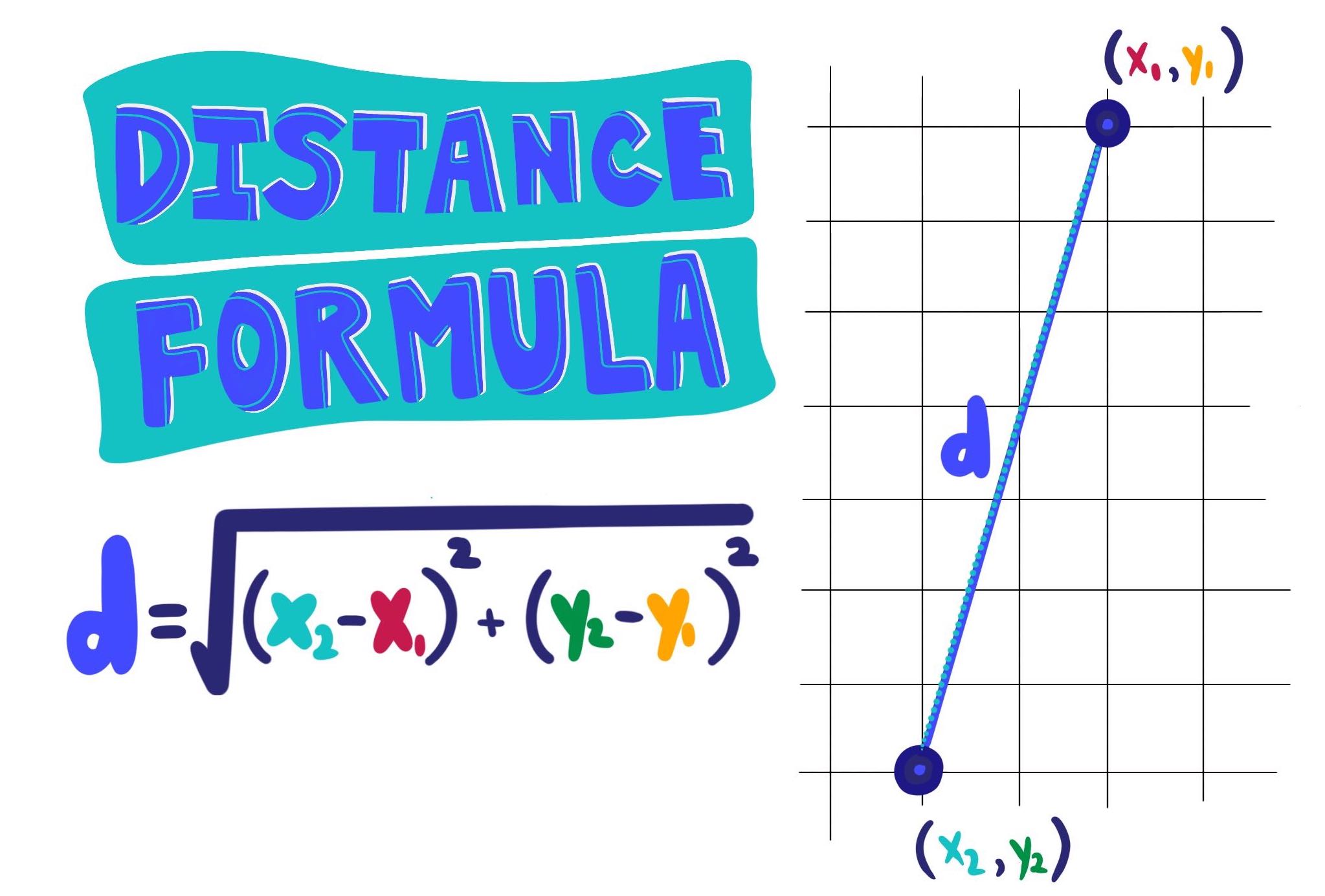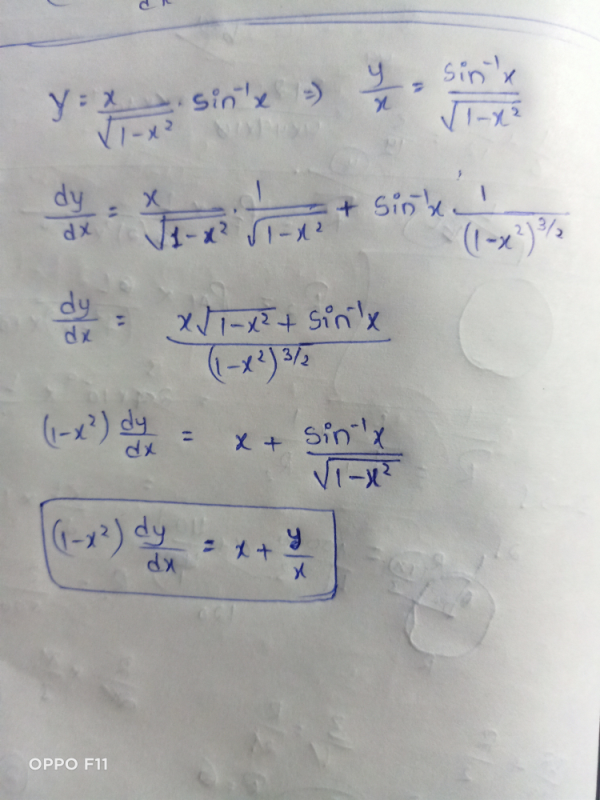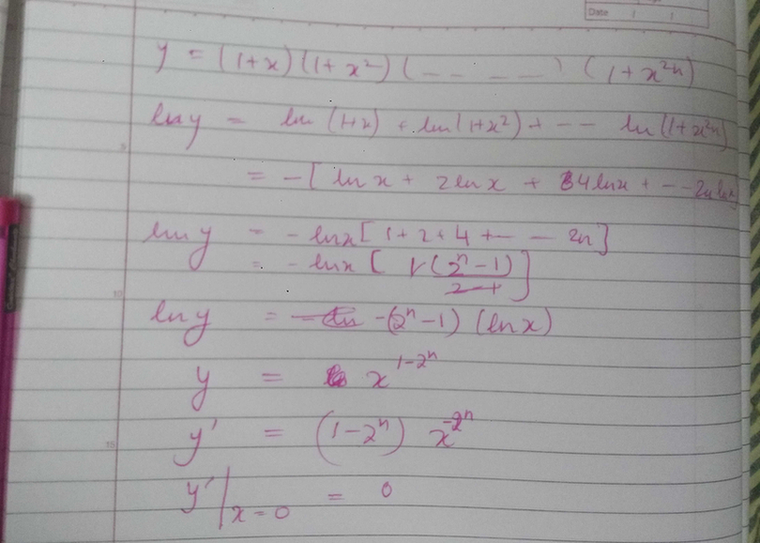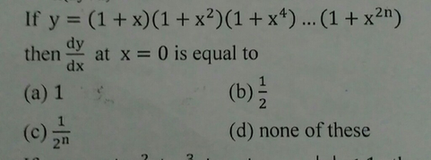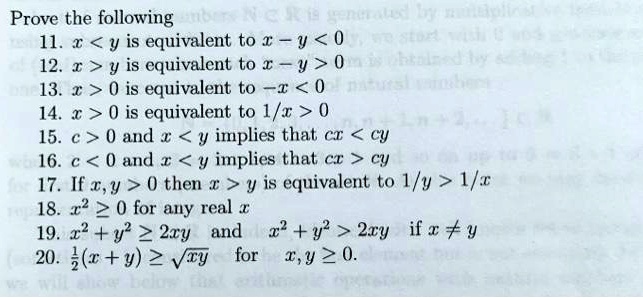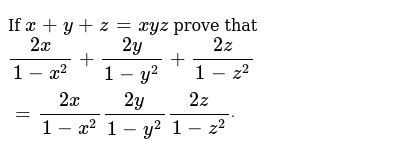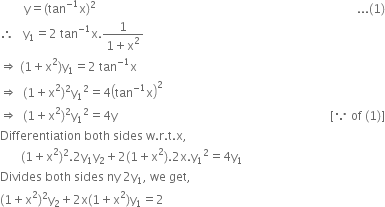「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Solved Solve By Cauchy Method X 2 Y 2xy 2y Xlnx If Y 1 1 And Y 1 0 Course Hero
Solved 1 Find A Series Solution Of X 4 Y 2xy 12y Chegg Com
Y Xy 3 1 X 2 1 2 Y 0 1 Harushley
2
Indefinite Integral Of 1 X Antiderivative Of 1 X Video Khan Academy
When X 2 Y 2 T 1 T And X 4 Y 4 T 2 1 T 2 Then How Do You Prove That Dy Dx 1 X 3y How Would You Solve This Quora
If X 1 Y Y 1 X 0 Then Prove That 1 X 2 Dydx 1 0
If Y Cos 1 X 2 Prove That 1 X 2 Frac D 2 Y Dx 2 Xfrac Dy Dx 2 0 Hence Find Y 2 When X 0 Snapsolve
Pdf Random Walk Weakly Attracted To A Wall Francois Dunlop Academia Edu
Solved A Evaluate Lim X Y 1 1 X 2y E Y Chegg Com
If U X 2tan 1 Y X Y 2tan 1 X Y Prove That 2u Y X X 2 Y 2 X 2 Y 2 Sarthaks Econnect Largest Online Education Community
If Y Log Root X 1 Root 2 Then Prove X X 1 2 Y2 X 1 2 Y1
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Prove That X 1 Y 1 X 1 X 1 Y 1 Y 1 X Y 2 Xy
Solved 1 Prove That Learning The Class Of Logistic Regressors Hw Rd 0 1 With Loss Function U Hw 2 Y Log 1 Exp Y W 2 A Y A Rd X 1 1 Via Erm Is
Ipe Material Notes
Btech Ii Engineering Mathematics Unit5
2
If Y 1x 1 X2 1 X4 1 X2n Then At X 0 Is Equal Scholr
Differential Calculus Ppt Video Online Download
1 1 1 4 Homework Solutions 2 2b Prove That Im Iz Re Z Write Z
Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
Msa3 Mathematics Statistic Assignment 3 Stats 7059 Studocu
2
If Y 1x 1 X2 1 X4 1 X2n Then At X 0 Is Equal Scholr
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Y Xy 3 1 X 2 1 2 Y 0 1 Harushley
If Y X Sqrt 1 X 2 M Prove That 1 X 2 Y2 Xy1 M 2y 0 Sarthaks Econnect Largest Online Education Community
Linear Programming Maximize X 1 X 2 X
Plotting X 2 Y 2 1 3 X 2 Y 3 0 Mathematics Stack Exchange
Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy
Binomial Expansion Formulas Derivation Examples
If Y Sin A Sin 1 X How Do You Prove That 1 X 2 D 2y Dx 2 X Dy Dx A 2y Quora
If 2y X 1 X 1 Show That 4 X2 1 D2y Dx2 4x Dy Dx Y 0 Brainly In
Bijection Function F X Y X Y 1 2x 2y 2 Mathematics Stack Exchange
Buku 1 Latihan Pak Tedy
Graphing Parabolas
Solved Prove The Following 11 X Y Is Equivalent To 1 Y 0 12 I Y Is Equivalent To 1 Y 0 13 I 0 Is
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Homogeneous Differential Equations
If X Sint Y Sinmt Prove That 1 X 2 D 2y Dx 2 X Dy Dx M 2 Y 0 Maths Continuity And Differentiability Meritnation Com
If Y 1 X 2 X 1 Y 2 1 Prove That Dydx 1 Y 21 X 2
Prove The Inequality X X 1 Y Y 1 Xy 1 X X 1 Y Y 1 Xy 1
Solved Use The Epsilon Delta Definition To Prove The Chegg Com
If X Y Z X Y Z Prove That 2x 1 X 2 2y 1 Y 2 2z 1 Z 2 2x 1 X 2 2y 1 Y 2 2z 1 Z 2 Dot
Partial Derivative Examples Math Insight
How Do You Find The Equation Of The Tangent Line To The Curve Y X 4 2x 2 X At 1 2 Socratic
How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic
If Y X 1 X 1 X 1 X Dot Prove That Dy Dx Y 2y X
Let X Y Z Be Real Numbers Each Greater Than 1 Prove That X 1 Y 1 Y 1 Z 1 Z 1 X 1 X 1 Y 1 Y 1 Z 1 Z 1 X 1 M Cube Mathematics By Maheshwari
How To Prove That 1 Z 1 X 2 Y If 5 X 3 Y 45 Z Quora
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

Worked Example Intercepts From An Equation Video Khan Academy
Please See This Question If X 2 X 1 Y 2 Y 1 X 2 X 1 Y 2 Y 1 Show That Xy 1 Mathematics Topperlearning Com V5k62qhh
2
The Diophantine Equation Y Y 1 Y 2 Y 3 3x X 1 X 2 X 3 Ponnudurai 1975 Journal Of The London Mathematical Society Wiley Online Library
If Y E Msin 1 X Prove That 1 X 2 D 2y Dx 2 X Dy Dx M 2y Youtube
If 2x 3y 12z Then Prove That 2 X 1 Y 1 Z Maths Number Systems Meritnation Com
Pdf Fermat S Congruence Modulo A Prime Power
Graph Graph Inequalities With Step By Step Math Problem Solver
If 1 X Y 1 2y 1 Y Z Are The Three Consecutive Terms Of An A P Prove That X Y And Z Are The Three Consecutive Terms Of A G P Sarthaks Econnect Largest
If Y Tan 1 X 2 Then Prove That 1 X2 2 Y2 2x 1 X2 Y1 2 From Mathematics Continuity And Differentiability Class 12 Up Board
1 Complex Numbers
Pdf Solvability For High Dimensional Fractional Differential Systems With High Arbitrary Orders
ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Prove that x^-1/x^-1 y^-1 x^-1/x^-1-y^-1=2y^2/y^2-x^2」の画像ギャラリー、詳細は各画像をクリックしてください。

15 Symmetric Polynomials Pdf Free Download
Abstraction Decomposition Relevance Coming To Grips With Complexity
Answered 2 14 Given That G X 1 X 1 3x2 A Bartleby
Assignment No

Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange texx ^ 2 xy y ^ 2 = \left x ^ 2 2 x \left( \frac{1}{2} y \right) \left( \frac{1}{2}y \right) ^ 2 \right \frac{3}{4} y ^ 2/tex I'm almost spilling out the answer Since the OP has already had his own solution, this is just another way to tackle the problem So, what left is to determine when the equation holds ) #9 njama 216 1 There is much easier way to

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)
close